Rechenschwache Grundschüler – Ursachen, Diagnose, Förderung

Prof. Dr. Oliver Thiel

Was ist Rechenschwäche?

Es ist unumstritten, dass es in der Schule immer wieder Kinder gibt, die besonders beim Rechnen oder allgemein im Mathematikunterricht besondere Schwierigkeiten haben, in anderen Lernbereichen jedoch nicht. Der Fachmann spricht dann von einer isolierten schulischen Minderleistung im mathematischen Bereich. Umgangssprachlich hat sich der Begriff Rechenschwäche (als Fremdwort auch Dyskalkulie) durchgesetzt, obwohl sich die Experten streiten, was genauer darunter zu verstehen ist (vgl. Lorenz 1991, S. 6). Eine ausführliche Diskussion dieses Definitionsproblems finden Sie in Thiel (2001, S. 10-20). In der Literatur findet man vor allem zwei grundsätzlich gegensätzliche Positionen: Die einen verstehen Rechenschwäche als mehr oder weniger konstante Persönlichkeitseigenschaft eines Menschen. Andere definieren Rechenschwäche eher phänomenologisch als Schwierigkeiten im Erlernen von Mathematik (z.B. Laschkowski 1992, S. 460), die prinzipiell jeder zeitweise bekommen kann.

Allen Definitionen, die Rechenschwäche als Persönlichkeitseigenschaft eines Schülers betrachten, kann man grundsätzlich vorwerfen, dass sie nur bedingt hilfreich sind, da sich aus der Diagnose einer Rechenschwäche keine handlungsleitenden Folgerungen ziehen lassen. Anders ist dies z.B. bei der Definition von Schulz (1995, S. 39), die Rechenschwäche als umgangssprachliche Bezeichnung für extreme Lernschwierigkeiten im Mathematikunterricht auffasst. Dabei soll mit der Wahl des Begriffs Lernschwierigkeiten deutlich gemacht werden, dass es sich weder um eine Einschätzung der Gesamtpersönlichkeit des Schülers noch um eine Krankheit handelt (Schulz 1995, S. 15). Durch diese Definition wird kein Schüler stigmatisiert, da nicht sein Versagen im Leistungsbereich als Kriterium herangezogen wird. Vielmehr wird ihm Hilfe angeboten.

Lernschwierigkeiten im Mathematikunterricht entstehen dadurch, dass die der Mathematik innewohnenden Hürden des Verstehens von einem Kind nicht bearbeitet wurden. Für viele Experten (z.B. Lerntherapeuten) stellen die folgenden Kernelemente der Arithmetik für viele Kinder solche Hürden beim Mathematiklernen dar (vgl. Meyerhöfer, 2008, S. 604):

• der kardinale und relationale Zahlbegriff
• die Logik des Stellenwertsystems
• die Operationslogik:

o Welche Fragen stellen die Rechenoperationen?
o Und auf welche Weise beantworten sie diese Fragen?
o Warum funktionieren die schriftlichen Rechenverfahren?
o manchmal insbesondere die Operationslogik der Division auch als Voraussetzung für die Bruchrechnung.

Von wissenschaftlicher Seite werden vor allem zwei „Nadelöhre“ (vgl. Gerlach/Fritz/Ricken/Schmidt, 2007) in den Blick genommen, die jedoch mit den oben genannten Kernelementen eng zusammen hängen:
• die Integration von Mengenvorstellungen und Wissen über Zahlen zum Kardinalzahlbegriff
• und das Teil-Teil-Ganzes-Konzept, denn

o dieses Konzept ermöglicht erst die Überwindung des zählenden Rechnens und die Entwicklung effektiver Rechenstrategien,
o und auf ihm bauen die weiterführenden Rechenoperationen auf.

Für Lehrer und Eltern betroffener Kinder sollte nicht so sehr die Frage im Mittelpunkt stehen, ob ein Kind rechenschwach ist oder nicht. Wichtiger ist, danach zu fragen, welche Lernschwierigkeiten das Kind im Mathematikunterricht hat (Diagnose) und wie ihm geholfen werden kann (Förderung). Die entscheidende Frage dabei ist, wo die Ursachen für das Versagen liegen.

Ursachen der Rechenschwäche

Es wird heute allgemein davon ausgegangen, dass die Ursachen für Minderleistungen im mathematischen Anfangsunterricht breit gefächert und vernetzt sind (vgl. Ellrott/Aps-Ellrott 1998, S. 3-8; Adelman 1989), sodass eine Aufzählung defizitärer Merkmalsbereiche als Ursachen für Lernschwierigkeiten nicht ausreicht (vgl. Schulz 1995, S. 18). Bei solchen Aufzählungen ist zudem meist das Zustandekommen der Listen unklar (vgl. Lorenz 1982, S. 199). Bevor ich ein Modell beschreibe, dass der derzeitigen Sicht auf Lernschwierigkeiten im Mathematikunterricht der Grundschule entspricht, möchte ich jedoch zunächst noch auf Grissemann (1989, S. 82) eingehen, der den umfassendsten Überblick zu vermuteten Ursachen der Rechenschwäche gibt.

1. Kongenitale (d.h. angeborene) Ursachen wurden noch in den siebziger Jahren des zwanzigsten Jahrhunderts als Hauptursache angenommen (Weinschenk 1970). Zwillingsstudien (Alarcón et al. 1997, S. 619f) zeigen jedoch, dass Umweltfaktoren eine größere Rolle spielen. Außerdem sind kongenitale Ursachen schwer nachzuweisen und für die Therapie kaum relevant, da sie sich im Nachhinein nicht mehr beeinflussen lassen.

2. Neuropsychologische Ursachen (d.h. Gehirnstörungen) werden heute noch oft angeführt (z.B. Nolte 2000, S. 31). Sie können sich in folgenden Schwierigkeiten äußern:

a. visuelle Wahrnehmungsstörungen
b. Speicherungsschwierigkeiten
c. Automatisierungsschwierigkeiten
d. impulsiver Kognitionsstil
e. grafomotorische Störungen
f. Richtungsstörungen des Rechnens

Die Untersuchung von Esser (1994, S. 56), bei der jedoch die Rechenschwäche nicht berücksichtigt wurde, lässt allerdings organische Defekte als Ursache oder wesentliche Mitursache von umschriebenen Entwicklungsverzögerungen unwahrscheinlich erscheinen.

3. Soziokulturelle und familiäre Bedingungen zeigen sich vor allem in folgenden Bereichen:

a. mangelnde Leistungsmotivation
b. impulsiver Kognitionsstil
c. Arbeitshaltung, Ausdauer
d. sprachliche Schwierigkeiten

Viele amerikanische Autoren schätzen die Bedeutung von psychosozialen Faktoren gering ein (z.B. Rourke 1989, Galaburda 1989). Nach der Untersuchung von Esser (1994, S. 57) haben sie jedoch eine nicht unwesentliche Bedeutung.

4. Schulische Ursachen sind Ursachen, die erst durch die Schulsituation wirksam sind, z.B.:

a. Lücken in den Basisoperationen durch mangelnde Beschulungskontinuität oder durch unterrichtliche Qualitätsmängel
b. mangelnde operative Flexibilität infolge Drillrechnens
c. erhöhte schulische Misserfolgsängstlichkeit

Gerster (1997, S. 10) meint sogar, dass Lernschwierigkeiten von Schülern immer Lehr-Lernschwierigkeiten sind. Schwarzer (1980, S. 116f) hebt insbesondere die Bedeutung von Vorkenntnislücken hervor und Kutzer (1999, S. 17f) führt Lernversagen auf didaktische Fehlentscheidungen zurück, die jedoch nicht primär den Lehrerinnen und Lehrern sondern dem lernpsychologischen und didaktischen Forschungsstand anzulasten sind.

5. Neurotisch-psychogene Ursachen beruhen auf psychischen Konflikten. Sie äußern sich in:

a. Ängstlichkeit
b. Angstabwehrmechanismen
c. Komplexbezügen zum Rechnen

Ungenügende Passung als Ursache der Rechenschwäche

Die moderne Mathematikdidaktik betrachtet Mathematiklernen als einen Entwicklungsprozess. Jedes Kind muss seinen eigenen Weg finden und sich ein eigenes Verständnis aufbauen. Bei Kindern mit Lernschwierigkeiten ist dieser Prozess zeitweise behindert. Die Ursachen für solche Lernschwierigkeiten sind im komplexen Zusammenwirken von verschiedenen Persönlichkeitsmerkmalen des Schülers mit den Bedingungen, unter denen der Lehr-Lern-Prozess stattfindet, zu sehen (Schulz 1994, S. 6, dort auch die Abbildung).

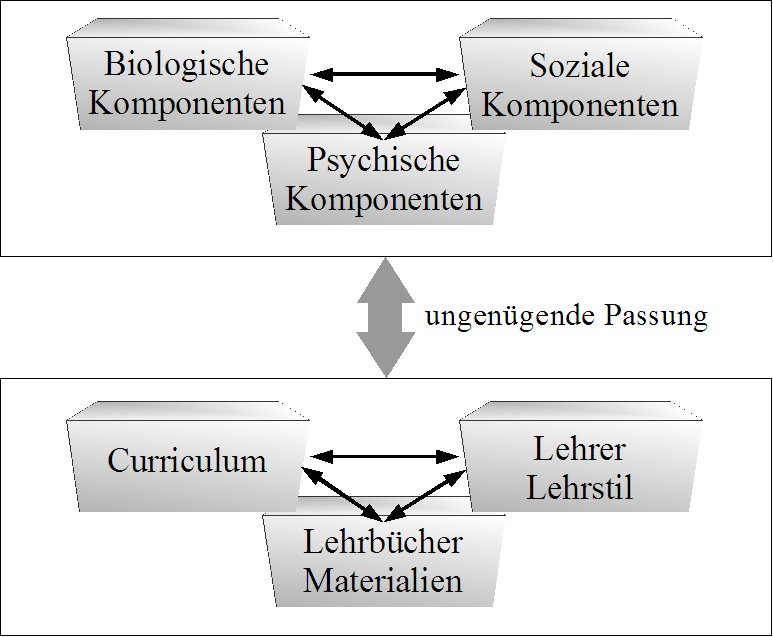
Lernschwierigkeiten treten also nur in konkreten Situationen unter bestimmten Bedingungen auf und müssen deshalb auch in diesen Situationen analysiert und charakterisiert werden. Erst eine ungenügende Passung der individuellen Lernvoraussetzungen des Schülers mit den Lernanforderungen, die an ihn gestellt werden, führt zum Auftreten und zur Verfestigung von Schwierigkeiten (Schulz 1994, S. 7, vgl. Gerster 1997, S. 10).

Diagnose der Rechenschwäche

Eine Diagnose dient dazu, Unterschiede zwischen verschiedenen Personen im Verhalten und Erleben zu erfassen sowie Veränderungen bestimmter Merkmale einer Person festzustellen. Das Ziel der Diagnose ist, geeignete Maßnahmen abzuleiten, so dass unerwünschte Zustände behoben werden. So ist das Ziel im Mathematikunterricht der Grundschule die Schwierigkeiten, die ein Kind beim Rechnen hat, zu analysieren, um sie zu beheben. Die Diagnose soll helfen, die richtigen Entscheidungen darüber zu treffen, ob eine spezielle Förderung dieses Kindes nötig ist und wie diese Förderung aussehen sollte.

Geht man vom Konzept der Lernschwierigkeiten aus, besteht die Aufgabe der Diagnose nicht darin, ein Kind als rechenschwach oder nicht zu etikettieren, sondern herauszufinden, welche mathematischen Konzepte das Kind nicht richtig erfasst hat. Meyerhöfer (2008, S. 603) spricht von „nicht bearbeiteten stofflichen Hürden“. Um dem Kind dann bei der Bearbeitung dieser Hürden helfen zu können, ist es außerdem wichtig zu ergründen, wo die Ursachen für die Lernschwierigkeiten liegen, d.h. welche Lernvoraussetzungen fehlen oder nicht ausreichend entwickelt sind. Hierfür sind informelle Fragen und Aufgaben besser geeignet als standardisierte Tests. Ich stelle hier exemplarisch drei Diagnoseverfahren vor.

KALKULIE

Das KALKULIE Diagnoseprogramm für rechenschwache Kinder ist Teil eines gleichnamigen Trainingsprogramms. Es kann sowohl als Einzeltestverfahren als auch als Screening für eine ganze Schulklasse eingesetzt werden, um abzuklären, welche Kinder spezielle Förderung benötigen. Das Diagnoseheft (Fritz/Ricken/Gerlach, 2007a) gibt es in zwei Formen (A und B). Heft B ist für eine Wiederholung der Diagnose zu einem späteren Zeitpunkt gedacht. Jedes Heft besteht aus drei Teilen, die sich auf unterschiedliche Schuljahre beziehen:

1) Teil 1 für den Schuleingang und das erste Schuljahr,
2) Teil 2 für das erste bis zweite Schuljahr
3) und Teil 3 für das zweite bis dritte Schuljahr.

Sie können aber auch anders eingesetzt werden, z. B. wenn man in höheren Schuljahren Kindern mit erheblichen Lernschwierigkeiten hat. Die drei Teile des Diagnosehefts entsprechen den drei Bausteinen des Trainingsprogramms (s.u.).

Die Handreichungen zum Diagnoseheft (Fritz/Ricken/Gerlach, 2007b) enthalten neben den Durchführungs- und Auswertungsvorschriften für den standardisierten Teil auch Hinweise für eine Strategieanalyse, d.h. es ist durch eine genaue Beobachtung des Kindes in der Bearbeitungssituation zum Teil möglich herauszufinden, wie das Kind verschiedene Aufgaben löst. Insofern verbindet das KALKULIE Diagnoseprogramm eine standardisierte Diagnostik mit Teilen einer qualitative Analyse. Durch die fundierte theoretische Einbettung des Programms ist es möglich, genau die kritischen Punkte herauszuarbeiten, an denen die Förderung ansetzen muss, für die ein entsprechendes Trainingsprogramm gleich mitgeliefert wird.

Förder/Diagnose Box Mathematik

Die Förder- und Diagnose-Box (Kaufmann/Lorenz, 2006) dient der zielgerichteten Beobachtung von einzelnen Kindern der Klassenstufen 1 bis 4. Dabei geht es nicht um das Festhalten von Symptomen, sondern darum, die Denkprozesse und sich entwickelnden Fehlvorstellungen des Kindes zu verstehen. Es wird ein breiter Diagnosebereich abgedeckt: visuelle Wahrnehmung, quantitative und räumliche Begriffe, Zahlverständnis, Operationsverständnis (inkl. Sachaufgaben), Rechnen und Rechenstrategien, Größen sowie Problemlösen. Die entsprechenden Beobachtungsbögen können unmittelbar nachdem ein Inhalt erarbeitet wurde zur Überprüfung des Lernerfolgs eingesetzt werden. Es ist aber auch die längerfristige Dokumentation der individuellen Lernentwicklung von Kindern möglich.

Das große Plus der Diagnosebox – nämlich ihre Vollständigkeit – ist gleichzeitig ihr größter Nachteil. Das angebotene Diagnose- und Fördermaterial ist so umfangreich, dass es eine intensive Einarbeitung in jedes einzelne Gebiet erfordert. Das sollte für professionelle Lerntherapeuten kein Problem sein. Lehrerinnen und Lehrer, die nur gelegentlich mit Lernschwierigkeiten zu tun haben, wird es aber abschrecken oder gar überfordern.

Eine quantitative Diagnostik ist mit der Diagnosebox nicht beabsichtigt. Mit ihrer Hilfe soll und kann jedoch entschieden werden, welche konkreten Maßnahmen zur individuellen Förderung eines Kindes ergriffen werden müssen. Dazu enthält die Box viele Fördervorschläge auf Karteikarten, die z.T. auch als Kopiervorlagen dienen. Sie können bei der Einzelförderung, teilweise auch zur Förderung in der ganzen Klasse eingesetzt werden. Das Handbuch enthält außerdem eine Kopiervorlage für die Erstellung individueller Förderpläne. Nachdem man sich mit dem zugrundeliegenden Förderkonzept vertraut gemacht hat, kann dies alles mit großem Gewinn eingesetzt werden.

Informelle Verfahren

Zu den für erfolgreiches Mathematiklernen nötigen Voraussetzungen gehören u.a.

• Orientierung (Körperschema, Raumorientierung),
• Vorstellung (Zahlvorstellungen, Größenvorstellungen, geometrische Vorstellungen),
• Konzentration,
• Abstraktion,
• Gedächtnis,
• visuelle Wahrnehmung und Sprache.

Defizite bei den mathematischen Konzepten lassen sich schon mit wenigen Aufgaben zuverlässig feststellen. Eine Sammlung solcher Aufgaben findet man z.B. bei Lorenz und Radatz (1993, S. 221-231).

Da für das Entstehen von Lernschwierigkeiten jedoch nicht allein die Fähigkeiten des Schülers verantwortlich sind, müssen auch Fragen zu Schule und Elternhaus gestellt werden. Anhaltende Misserfolgserlebnisse im Mathematikunterricht können zu Schulunlust oder gar Angst vor der Schule oder zu einer ablehnenden Haltung gegenüber dem Mathematikunterricht oder der Mathematiklehrerin führen. Umgedreht kann aber auch eine anders begründete Schulangst dazu führen, dass ein Kind die Beschäftigung mit mathematischen Inhalten vermeidet, so dass Lernschwierigkeiten entstehen. Ursachen können eine Außenseiterrolle in der Klasse oder Probleme in der Familie sein. Ein Erziehungsstil, der die Selbstständigkeit eines Kindes stark einschränkt oder es unter großen Leistungsdruck setzt, kann die Verfestigung von Lernschwierigkeiten begünstigen. Dagegen gibt die Frage nach den Lieblingsfächern und Lieblingsbeschäftigungen des Kindes Aufschluss über seine Stärken, die in der Therapie zur Entwicklung von Selbstwert und Motivation genutzt werden können.

Hinweise auf mögliche Schwierigkeiten können aufmerksame Eltern, Erzieherinnen und Lehrerinnen jedoch auch selbst sammeln (vgl. Lorenz/Radatz 1993, S. 36-80). Schon im Vorschulalter kann man die Kinder beim Memory-Spielen, Puzzeln, Bauen mit Klötzen, Nachzeichnen, Schleifen- und Schnürsenkelbinden und Sprechen beobachten. In der ersten und zweiten Klasse sollten die Kinder durch die Grundschullehrerin beobachtet werden. Wie geht das Kind mit Spielmaterial um? Wie sehen seine Zeichnungen aus? Kann es sich orientieren? Hat es Probleme mit dem Zehnerübergang oder mit der Bündelung? Lorenz und Radatz (1993) beschreiben, wie ein Mathematikprofil erstellt werden kann (S. 49) und wie Schülervorstellungen von Zahlen und Rechenoperationen analysiert werden (S. 51).

Förderung rechenschwacher Grundschüler

Förderprogramme, die rechenschwachen Kindern helfen, ihre Schwierigkeiten zu überwinden, müssen neben allgemeinen Maßnahmen, die alle Lernschwierigkeiten betreffen, insbesondere eine intensive Arbeit an den mathematischen Inhalten enthalten, die auf die speziellen Probleme des betroffenen Kindes abgestimmt ist. Bei vielen rechenschwachen Kindern ist insbesondere die Entwicklung der folgenden Bereiche wichtig:

1. Zahlvorstellungen
2. Handlungsvorstellungen zu Rechenoperationen
3. Effektive Rechenstrategien

Es gibt sehr viele Veröffentlichungen von Förderprogrammen, so dass es an dieser Stelle nicht möglich ist, einen kompletten Marktüberblick zu geben. Ich werde deshalb nur exemplarisch einzelne Werke, mit denen ich Erfahrungen habe, nennen und kommentieren. Im Anschluss werde ich ein Konzept näher vorstellen, nach dem ich selbst als Lerntherapeut gearbeitet habe.

KALKULIE

Auch das KALKULIE Trainingsprogramm (Gerlach/Fritz/Ricken/Schmidt, 2007) gehört zum bereits vorgestellten Diagnoseprogramm. In verschiedenen Modulen werden unterschiedliche Fördermöglichkeiten angeboten – abgestimmt auf die jeweilige Kompetenzstufe des Kindes. Die Aufgaben können hinsichtlich der Repräsentationsebene (Handlungsebene, bildliche und symbolischen Ebene) und des verwendeten Zahlenraumes variiert werden.
Das Förderprogramm besteht aus drei Bausteinen, die jeweils drei Untergruppen von Anforderungen enthalten:

1) Baustein 1 behandelt fertigkeitsspezifische Voraussetzungen und enthält 42 Kopiervorlagen zu 35 Erarbeitungs- und 21 Übungsaufgaben aus den Bereichen Reihen bilden und Zählen, Mengenaspekte und Kardinalität sowie Zahlen- und Mengenwissen integrieren.
2) Baustein 2 behandelt Strukturen im Zwanzigerraum und enthält 26 Kopiervorlagen zu 23 Erarbeitungs- und 15 Übungsaufgaben aus den Bereichen Strukturen erkennen und herstellen, Strukturen geschickt nutzen sowie Strukturen flexibilisieren.
3) Baustein 3 behandelt Nicht-zählende Rechenstrategien im Zwanzigerraum und enthält 41 Kopiervorlagen zu 34 Erarbeitungs- und 24 Übungsaufgaben aus den Bereichen Strategien „Kraft der 5“ und „Kraft der 10“ festigen, Teil-Teil-Ganzes-Beziehungen verstehen sowie Rechenfakten erwerben.

Die vorgeschlagene Förderung wird übersichtlich und verständlich dargestellt. Alle Fördervorschläge sind in den theoretischen Ausführungen verankert, so dass eine Förderung bewusst an den kritischen Stellen ansetzen kann. Weiterführende Aufgabenstellungen und Variationen werden angeboten, wenn Kinder bestimmte Aufgaben gut bewältigen oder zusätzliche Materialien brauchen. Strategieanalysen gibt es nicht nur für die Diagnoseaufgaben sondern auch für die Beobachtungen, die während der Förderung gemacht werden. Sie beziehen sich nicht nur auf Lösungen, sondern auch auf die Bearbeitungsweisen von Aufgaben.

Das Programm ermöglicht es sowohl Lerntherapeuten als auch Lehrerinnen und Lehrern die eigene Herangehensweise an eine Förderung zu reflektieren und neues in eigene bewährte Techniken zu integrieren – aber auch Förderung von Grund auf neu zu konzipieren.

Förder/Diagnose Box Mathematik

Die Förder- und Diagnose-Box (Kaufmann/Lorenz, 2006) wurde schon bei den Diagnoseinstrumenten ausführlich beschrieben, so dass ich mich hier kurz fassen kann. Die Box enthält ein Wimmelbild DIN A1 und 208 Karteikarten mit Förderideen (teilweise mit Kopiervorlagen). Nachdem die Diagnose durchgeführt wurde, kann man dem Beobachtungsbogen genaue Hinweise entnehmen, welche Förderideen für das betroffene Kind hilfreich sind. Es werden alle Bereiche der Grundschulmathematik (Klasse 1 bis 4) einschließlich der kognitiven Voraussetzungen abgedeckt.

Trainieren mit Einstein

Die Grundlagen für das Förderprogramm (Grassmann/Thiel, 2006a, 2006b), wurden u.a. von Frau Dr. Andrea Schulz (1995) entwickelt (vgl. Thiel 2000, 2002).

Zahlvorstellungen

Der Zahlenraum bildet die Grundlage für die Erarbeitung von Rechenstrategien. Das Wort Zahlenraum deutet an, dass Zahlen nicht als voneinander unabhängige abstrakte Objekte aufgefasst werden, sondern in Beziehung zueinander stehen. Die Schüler sollen lernen, sich im Zahlenraum zu orientieren. Damit ein Kind die Strukturen des Zahlenraums erkennen kann, wird der Zahlenraum in Abschnitten ganzheitlich erarbeitet. Für die Zahlen bis 10 sind die Finger das wichtigste Arbeitsmittel, wobei ganzheitlich bedeutet, dass alle zehn Finger einbezogen und nicht dynamisch, sondern statisch benutzt werden. Die Finger werden also nicht (wie beim Zählen) sukzessive aufgeklappt, sondern das Kind zeigt Anzahlen, die Dank der Fünferstruktur der Finger simultan erfasst werden können (vgl. Lorenz/Radatz 1993. S.181). Die gleiche Struktur sollte auch eine Legekette mit verschiedenfarbigen Perlen aufweisen. Auch beim Darstellen der Zahlen mit Hilfe der Würfelbilder wird die Kraft der Fünf genutzt, d.h. die sechs ist eine 5+1 (nicht wie auf dem Würfel eine 3+3).
Die folgende Abbildung zeigt die Darstellung der Zahl 6 in Grassmann/Thiel (2006, S. 10):

Diese Würfelbilder werden von den Kindern nicht nur gemalt, sondern auch mit Holzklötzchen gespürt, gelegt und verändert.
Verdoppelung der Anzahl von zehn Gegenständen führt zu den Zahlen bis 20, die erste Einblicke in die dekadische Struktur gewähren. Die Analogien zwischen den Zahlen von 1 bis 10 und von 11 bis 20 können auch die meisten rechenschwachen Kinder schnell entdecken. Der Zahlenraum bis 100 kann sehr schön mit einem teilweise mit Zahlen gefüllten Hundertertafel eingeführt werden, das in Streifen zerschnitten wird: 10 Papierstreifen, die je 10 Kreise tragen, in die an den Rändern Zahlen eingetragen sind (1 und 10, 11 und 20 usw.) Aus den Streifen kann zunächst ein Zahlenstrahl gelegt werden. Schließlich werden die Streifen (um Platz zu sparen) zur Hundertertafel (Lorenz/Radatz 1993, S. 102) zusammengeschoben. Hier können die Kinder Strukturen entdecken und haben manches Aha-Erlebnis. Auf der Hundertertafel können auch Orientierungsübungen durchgeführt werden, z.B. “Wo steht die 53? Welche Zahl steht darüber, welche darunter, welche kommt davor und welche kommt danach?” Ein Pfeil über der Tafel erleichtert Kindern mit Orientierungsproblemen das Einhalten von Richtungen.

Neben der Hundertertafel sind das Hunderterfeld (ohne Zahlen) und die Mehrsystemblöcke nach Dienes (Lorenz/Radatz 1993, S. 101) die wichtigsten Arbeitsmittel im Zahlenraum bis 100. Beide dienen zum Darstellen von Anzahlen, wobei das Dienes-Material in seiner Genialität kaum übertroffen werden kann. Es entspricht in seiner Struktur dem goldenen Perlenmaterial nach Montessori und spiegelt nämlich nicht nur die Zehnerbündelung (Einerwürfel, Zehnerstangen, Hunderterplatten) richtig wieder, sondern auch die Dreiergruppierung von Stellen bei größeren Zahlen, wobei Einer- und Tausenderwürfel, Zehner- und Zehntausenderstangen und Hunderter- und Hunderttausenderplatten einander entsprechen (Schlüter, 2010a). Diese Analogie können die Kinder entdecken und nutzen, wenn sie sich den Zahlenraum bis eine Million erarbeiten (Schlüter, 2010b).

Handlungsvorstellungen zu Rechenoperationen

Ein typisches Merkmal von Kindern mit Lernschwierigkeiten im Mathematikunterricht ist das zählende Rechnen (Schipper, 2001, S. 11).Um rechenschwachen Grundschülern über das zählende Rechnen hinwegzuhelfen, ist es nötig, die Rechenoperationen mit Handlungen zu verknüpfen, die aus dem Alltag stammen und auf die effektive Rechenstrategien aufgebaut werden können. Zur Verinnerlichung von Operationen bietet sich die folgende Stufenfolge an (vgl. Aebli, 2006, S. 238f):

1) Alltagshandlungen (mit Sprachhandlung jeweils parallel auf allen Ebenen)
2) Standardhandlung mit strukturiertem Material
3) Wahrnehmungshandlung
4) geistige Handlung

Dabei ist der Therapeut auf die Mitarbeit der Eltern angewiesen, die ihrem Kind in vielfältigen Alltagssituationen zeigen können, wie diese als Addition, Subtraktion, Multiplikation oder Division gedeutet werden können.
Addition und Subtraktion besitzen immer einen dynamischen oder einen statischen Aspekt. Beim dynamischen Aspekt ändert sich etwas: Dinge werden hinzugelegt oder weggenommen, hinzugekauft oder verkauft, Kinder kommen hinzu oder gehen weg, stellen sich an, steigen ein oder aus, … Beim statischen Aspekt wird festgestellt, wie der Zustand ist, die Situation ändert sich dabei nicht: Auf dem Tisch liegen drei rote und fünf blaue Plättchen. Zusammen sind es acht Plättchen. Es sind zwei blaue Plättchen mehr als rote. In der Klasse sind 11 Mädchen und 13 Jungen. Zusammen sind es 24 Kinder. Es sind zwei Jungen mehr als Mädchen. Beide Aspekte sollten jeweils getrennt eingeführt werden, wobei der Schwerpunkt auf dem dynamischen Aspekt liegen sollte.

Multiplikationen können zeitlich sequentielle Abläufe (z. B.: Paula geht dreimal in den Keller und bringt bei jedem Mal zwei Flaschen Saft mit hoch.), räumlich gegliederte Muster (z. B.: Auf der Tanzfläche tanzen drei Pärchen.) und Kombinationen (z. B.: Paula hat zwei Röcke und drei Blusen.) repräsentieren. Nur zeitliche Abläufe sind konkrete Handlungen. Folglich wird damit begonnen.

Räumliche Muster sind oft das Ergebnis von konkreten Handlungen. Wenn ich viermal einen Turm aus drei Bausteinen baue, so stehen schließlich viermal drei Bausteine auf dem Tisch. Eine sinnvolle Handlung für Schülerinnen und Schüler besteht auch darin, räumlich gegliederte multiplikative Muster in der Umwelt zu suchen, z. B. an Häuserfassaden oder in Verpackungen. Die Kinder sind dann „Mal-Detektive“ oder tragen eine selbst gebastelte „Mal-Brille“, mit der man Malaufgaben besser erkennen kann. Kombinationen sind so abstrakt, dass sie an dieser Stelle noch nicht behandelt werden sollten. Bei der Division unterscheidet man das Verteilen und das Aufteilen. Beim Ersten werden die Elemente einer Menge an eine vorgegebene Zahl von Teilmengen verteilt und gefragt, wie viele Elemente jede Teilmenge erhält, z. B.: 24 Kinder sollen sich gleichmäßig auf 6 Zimmer verteilen. Wie viele Kinder kommen in jedes Zimmer? Beim Zweiten wird eine Menge in gleichgroße Teilmengen aufgeteilt und gefragt, wie viele Teilmengen man erhält, z. B.: 24 Kinder fahren auf Klassenfahrt. Immer 6 Kinder können zusammen in einem Zimmer schlafen. Wie viele Zimmer werden benötigt? Bei den Alltagshandlungen sollten beide Aspekte in gleicher Weise berücksichtigt werden. Die Kinder müssen sie jedoch nicht begrifflich unterscheiden können.

Am Anfang stehen also immer konkrete Handlungen mit Alltagsmaterialien. Dabei ist die Mitarbeit der Eltern hilfreich, die ihrem Kind in vielfältigen Alltagssituationen zeigen können, wie diese als Addition, Subtraktion, Multiplikation oder Division gedeutet werden können. In einem Schulbuch oder Arbeitsheft können nur Bilder dargestellt werden. Um den Handlungscharakter deutlich zu machen, werden bei der Einführung einer neuen Operation Bildgeschichten gezeigt, die schrittweise zu statischen Bildern verkürzt werden, in die von den Kindern Handlungen hinein gesehen werden müssen. Mit Sprachhandlung ist gemeint, dass die Kinder die Operation, die sie handelnd durchgeführt oder auf einem Bild erkannt haben, mit eigenen Worten beschreiben, um sie sich selbst bewusst zu machen. Dabei wird gleichzeitig die allgemeine mathematische Kompetenz des Kommunizierens entwickelt: Die Kinder beschreiben eigene Vorgehensweisen, verstehen die Lösungswege der anderen und reflektieren gemeinsam darüber. Außerdem lernen sie, die mathematische Fachbegriffe („plus“, „minus“ und „gleich“) sachgerecht zu verwenden.

Auch auf der zweiten Stufe wird noch handelnd gearbeitet – nun aber mit strukturiertem Material. Mit der Standardhandlung sind alle Aufgaben ohne zu zählen lösbar. Für den Aufbau von Rechenstrategien bietet sich folgende Handlung zur Addition und Subtraktion an:

• In einem Warenlager liegen x Kisten (dargestellt durch strukturiert angeordnetes Material).
• Ein LKW (auf Papier aufgemalt) bringt (Addition) oder holt (Subtraktion) y Kisten.
• Wie viele Kisten im Lager verbleiben, kann man sehen, ohne zählen zu müssen.

Multiplikative Strukturen lassen sich durch Würfeltürmchen, Punktfelder (Ausschnitte aus dem Hunderterfeld) oder mit Dienes-Material darstellen. Divisionen werden hauptsächlich durch Verteilen (seltener durch Aufteilen) von Dienes-Material gelöst.

Aebli (2006, S. 238f) spricht von Wahrnehmungshandlung, wenn die Lösungswege, die beim handelnden Umgang mit strukturiertem Material entdeckt wurden, bildlich dargestellt und mit Worten beschrieben werden. Die bildliche Darstellung sollte der Standardhandlung möglichst entsprechen und von den Kindern selbst ausgeführt werden können.

Sind solche grundlegenden Vorstellungen zu den Rechenoperationen aufgebaut, lassen sich diese mühelos auf größere Zahlenräume übertragen:

Grundaufgabe	analoge Aufgaben
4 + 3	40 + 30	84 + 3	48 + 30
8 - 3	80 - 30	48 - 3	84 - 30
3 x 4	3 x 40	3 x 400
9 : 3	90 : 3	900 : 3

 

Effektive Rechenstrategien

In vielen Fällen stellt die Zehnerüberschreitung eine Hürde im Lernprozess dar. Ohne vorherige Erarbeitung von Handlungsvorstellungen werden viele rechenschwache Kinder eine Aufgabe wie 8 + 6 nur zählend lösen können. Bei 28 + 6 ist man mit dieser Strategie noch relativ sicher. Bei 28 + 16 braucht man schon sehr lange und verzählt sich meist. Bei 28 + 26 ist es fast unmöglich auf diesem Wege zu einer Lösung zu gelangen. Man könnte versucht sein, die „Stellenwerte extra“ zu addieren: 2 + 2 = 4 und 8 + 6 = 14, aber das führt nicht zwangs-läufig auf 54. Für Kinder mit Lernschwierigkeiten kann es auch 44 oder 414 oder 18 sein oder sie verzählen sich, wenn sie von 40 um 14 weiterzählen. Zählendes Rechnen kann also auf die Dauer zur Verfestigung einer Rechenschwäche führen (Schipper 2001, S. 11). Strukturierte Arbeitsmittel und Zahlvorstellungen erlauben operative Zusammenhänge zu sehen:

Rechenwege für 8 + 6
Zahlenbild	Rechenweg	Bezeichnung
	5 + 5 + 3 + 1	Kraft der Fünf
	6 + 6 + 2	Verdoppeln
	7 + 7	gegensinniges Verändern
	8 + 2 + 4	Ergänzen zum Zehner

 

Aber ich kann von einem rechenschwachen Kind nicht erwarten, dass es den für sich jeweils günstigsten Weg ohne Hilfe findet. Deshalb sollte man rechenschwache Kinder eine Rechenstrategie entdecken lassen, die sehr effektiv ist, und immer angewendet werden kann. Oft reicht schon ein kleiner Hinweis aus: „Was ist denn hier anders als bei den Aufgaben, die du schon kennst? Wie viel kannst du ohne Schwierigkeiten zur 8 dazu tun?“ Für Kinder mit Lernproblemen ist nach meinen Erfahrungen das Ergänzen zum Zehner der offensichtlichste Weg. In seltenen Fällen nutzen sie auch die Kraft der Fünf. Auch hier kann der LKW als Hilfe genutzt werden:

• Im Lager liegen acht Kisten, der LKW bringt sechs weitere.
• Ich lade zunächst zwei Kisten ab, denn 8 + 2 sind 10. Das kann man sehen. Hilfreich sind hier auch die Finger (vgl. Lorenz/Radatz 1993. S.181).
• Auf dem LKW verbleiben vier Kisten. Werden diese noch abgeladen, hat man zusammen 14.

Die Lösungswege, die beim handelnden Umgang mit konkretem Material entdeckt wurden, werden bildlich dargestellt und mit Worten beschrieben, um sie den anderen Kindern mitteilen zu können. Dies sind aber auch wichtige Schritte auf dem Weg zu mentalen Operationen. Die Verinnerlichung erfolgt (in Anlehnung an Aebli 1981) in vier Phasen von wachsender Schwierigkeit (vgl. Lorenz/Radatz 1993, S. 169-174):

1. Direkt nach der tatsächlichen Ausführung der Handlung beschreibt das Kind diese mit seinen eigenen Worten. Dazu ist eine innere Rekonstruktion der Handlung nötig, die sich auf die Wahrnehmung ihres konkreten Ergebnisses stützt.
2. Nur noch die Ausgangssituation wird mit Material dargestellt. Das rechenschwache Kind beschreibt die Handlung mit eigenen Worten, ohne sie tatsächlich auszuführen. Dazu muss die Handlung in Gedanken vorausgesehen werden.
3. Mit verbundenen Augen beschreibt das Kind die Handlung mit eigenen Worten, während jemand anderes (der Therapeut oder ein Mitschüler) die Handlung nach seinen Anweisungen ausführt. Dabei wird die Operation vom Schüler nur noch in Gedanken ausgeführt.
4. Schließlich kann die Handlung ganz ohne materielle Stütze mental ausgeführt und mit Worten beschrieben werden. Die Kinder gelangen verschieden schnell dahin, dass sie Aufgaben allein im Kopf lösen können.

Wenn ein rechenschwaches Kind die Addition ohne Zehnerüberschreitung im Zahlenraum bis 10, dazu analoge Aufgaben im Zahlenraum bis 100 und Aufgaben mit Zehnerüberschreitung im Zahlenraum bis 20 beherrscht, stellen Aufgaben mit Zehnerüberschreitung im Zahlenraum bis 100 (z.B. 48 + 36) nur noch eine kleine Hürde dar, da zu ihrer Lösung nur noch bekannte Verfahren kombiniert werden müssen:

1. Zerlegung des zweiten Summanden in Zehner und Einer (48 + 30 + 6)
2. 48 + 30 wird analog zu 4 + 3 gelöst
3. 58 + 6 wird analog zu 8 + 6 gelöst

Beispiele sollen verdeutlichen, wie diese effektive Rechenstrategie für andere Rechenoperationen funktioniert. Sie lassen sich ebenfalls leicht mit Dienes-Material erarbeiten.

Operation	Beispiel	Rechenschritte
Subtraktion	62 - 25	62 - 20	42 - 2	40 - 3
Multiplikation	3 x 14	3 x 10	3 x 4	30 + 12
Division	48 : 3	30 : 3	18 : 3	10 + 6

Literatur

• Adelman, H. S. (1989): Beyond the learning mystique: An interactional perspective on learning disabilities. In: Journal of Learning Disabilities. 22, S. 301-304.
• Alarcón, M./DeFries, J. C./Light, J./Pennington, B. F. (1997): A Twin Study of Mathematics Disability. In: Journal of Learning Disabilities. 30, (6), S. 617-623.
• Aebli, H. (2006): Zwölf Grundformen des Lehrens. Eine allgemeine Didaktik auf psychologischer Grundlage. 13. Aufl. Stuttgart.
• Ellrott, D./Aps-Ellrott, B. (1998): Förderdidaktik. Mathematik Primarstufe. 2. Aufl., Offenburg.
• Esser, G. (1994): Die Bedeutung organischer und psychosozialer Risiken für die Entstehung von Teilleistungsschwächen. In: Frühförderung interdisziplinär. 13, S. 49-60.
• Fritz, A./Ricken, G./ Gerlach, M. (2007a): Kalkulie – Testhefte. Diagnose- und Trainingsprogramm für rechenschwache Kinder. Diagnoseheft A. Berlin.
• Fritz, A./Ricken, G./ Gerlach, M. (2007b): Handreichung zur Durchführung der Diagnose. Kalkulie. Diagnose- und Trainingsprogramm für rechenschwache Kinder. Berlin.
• Galaburda, A. M. (1989): Learning disability: Biological, societal, or both? A response to Gerald Coles. In: Journal of Learning Disabilities. 22, S. 278-281.
• Gerlach, M./Fritz, A./Ricken, G./Schmidt, S. (2007): Trainingsprogramm Kalkulie. Diagnose- und Trainingsprogramm für rechenschwache Kinder. Baustein 1. Berlin.
• Gerster, H. D. (1997): Positionspapier. In: Abaküs(s)chen. (1), S. 10.
• Grassmann, M./Thiel, O. (2006a): Trainieren mit Einstein 1/2. Aufgaben zum Fördern und Festigen. Braunschweig.
• Grassmann, M./Thiel, O. (2006b): Trainieren mit Einstein 3/4. Aufgaben zum Fördern und Festigen. Braunschweig.
• Grissemann, H.(1989): Dyskalkulie heute: Forschungsgrundlagen der Dyskalkulietherapie. In: Zentralblatt der Mathematikdidaktik. (3), S. 76-84.
• Kutzer, R. (1999): Überlegungen zur Unterrichtsorganisation im Sinne strukturorientierten Lernens. In: Probst, H. (Hrsg.): Mit Behinderungen muss gerechnet werden. Der Marburger Beitrag zur lernprozessorientierten Diagnostik, Beratung und Förderung. S. 15-69, Solms-Oberbiel.
• Kaufmann, S./Lorenz, J.H. (2006): Förder/Diagnose Box Mathematik. Braunschweig.
• Laschkowski, W. (1992): Rechenstörungen – Bedingungen, Diagnostik und Möglichkeiten der Beeinflussung. In: Sachunterricht und Mathematik in der Primarstufe. 20, (10), S. 459-466.
• Lorenz, J. H. (1982): Lernschwierigkeiten im Mathematikunterricht der Grundschule und Orientierungsstufe. In: Bauersfeld, H.: Analysen zum Unterrichtshandeln. S. 168-209, Köln.
• Lorenz, J. H. (1991): Rechenschwache Schüler in der Grundschule – Erklärungsversuche und Förderstrategien, Teil I. In: Journal für Mathematikdidaktik. (1), S. 3-34, Paderborn.
• Lorenz, J. H./Radatz, H. (1993): Handbuch des Förderns im Mathematikunterricht. Hannover.
• Meyerhöfer, W. (2008): Vom Konstrukt der Rechenschwäche zum Konstrukt der nicht bearbeiteten stofflichen Hürden. In: Vásárhelyi, E. (Hrsg.): Beiträge zum Mathematikunterricht 2008, Münster, S. 601-604.
• Nolte, M. (2000): Marek hat keine Rechenschwäche entwickelt. In: Grundschulunterricht. 47, (7-8), S. 30-32.
• Rourke, B. P. (1989): Cole´s learning mystique: The good, the bad, and the irrelevant. In: Journal of Learning Disabilities. 22, S. 274-277.
• Schipper, W. (2001): Offenheit und Zielorientierung. In: Grundschule 33, (3), S. 10-15, Braunschweig.
• Schlüter, H. (2010): Strukturierte Materialien zur Zahlbereichserweiterung. In: Mathematik differenziert (2), S. 14-15.
• Schlüter, H. (2010): Erste Schritte bis zu einer Million. In: Mathematik differenziert (2), S. 32-36.
• Schulz, A. (1994): Fördern in Mathematik. Was kann ich tun? Berlin.
• Schulz, A. (1995): Lernschwierigkeiten im Mathematikunterricht der Grundschule. Berlin.
• Schwarzer, Ch. (1980): Gestörte Lernprozesse: Analyse von Leistungsschwierigkeiten im Schulsystem. München, Wien, Baltimore.
• Thiel, O. (2000): Von FÜNF auf EINS. In: Grundschulunterricht, 47, (7-8), S. 40-41.
• Thiel, O. (2001): Rechenschwäche und Basisfunktionen. Volxheim.
• Thiel, O. (2002): Wie rechnet man 28 + 27? Zum Konflikt zwischen Förderung der Beweglichkeit beim Rechnen und der Entwicklung effektiver Rechenstrategien. In: Grundschulunterricht, 49, (10), S. 21-24.
• Weinschenk, C. (1970): Rechenstörungen. Ihre Diagnostik und Therapie. Stuttgart, Wien.

Weitere Beiträge des Autors hier in unserem Familienhandbuch

• Lernschwierigkeiten

Autor

Oliver Thiel
A.o. Professor für Mathematik und ihre Didaktik an der Dronning Mauds Minne Hochschule für Kindergartenlehrerausbildung in Trondheim, Norwegen.
Der Autor arbeitet in der ersten Phase der Lehrerbildung und trägt durch eine fachlich fundierte Ausbildung von Erzieherinnen und Erziehern dazu bei, dass Rechenschwächen vorgebeugt wird.

Kontakt

Oliver Thiel
Dronning Mauds Minne Høgskole for barnehagelærerutdanning
Matematikkseksjonen
Thrond Nergaards veg 7
7044 Trondheim
NORWEGEN

E-Mail
Website

Erstellt am 28. Januar 2003, zuletzt geändert am 20. Mai 2015